Пусть \(k_0\) — корень уравнения \(f(k) = k\). Показать, что:
1) если \(f'(k_0)\lt 1\), то ни одно решение уравнения \(y' = f(y/x)\) не касается прямой \(y = k_0x\) в начале координат;
2) если \(f'(k_0)\gt 1\), то этой прямой касается бесконечно много решений.
Решение
Для начала рассмотрим геометрическую интерпретацию задачи.
Уравнение \(y' = f(y/x)\) является однородным дифференциальным уравнением. Изоклины уравнения имеют вид \(f(y/x)=k\), где \(k\) - постоянная.
Получаем, что изоклинами однородного дифференциального уравнения являются прямые проходящие через начало координат \(y=ax\), где \(a=f^{-1}(k)\).
Тангенс угла между прямой \(y=ax\) и пересекающей его интегральной кривой уравнения \(y' = f(y/x)\) равен \((f(a)-a) / (1+ af(a))\), соответственно если \(k_0\) — корень уравнения \(f(k) = k\), то \(y=k_0x\) это изоклина для которой угол между ней и интегральными кривыми равен нулю.
Рассмотрим пример:
\[y'=2\frac{y^2}{x^2}-\frac{y}{x}\]
\[f(k)=2k^2-k\]
Найдем решение уравнения \(f(k) = k\):
\[2k^2-k=k \ \Rightarrow \ k(k-1)=0 \ \Rightarrow \ k_0=0; k_0=1\]
Найдем \(f'(k_0)\):
\[f(k)=2k^2-k \ \Rightarrow \ f'(k)=4k-1\]
Получаем: \(f'(0)=-1\) и \(f'(1)=3\).
Построим приближенно интегральные кривые:
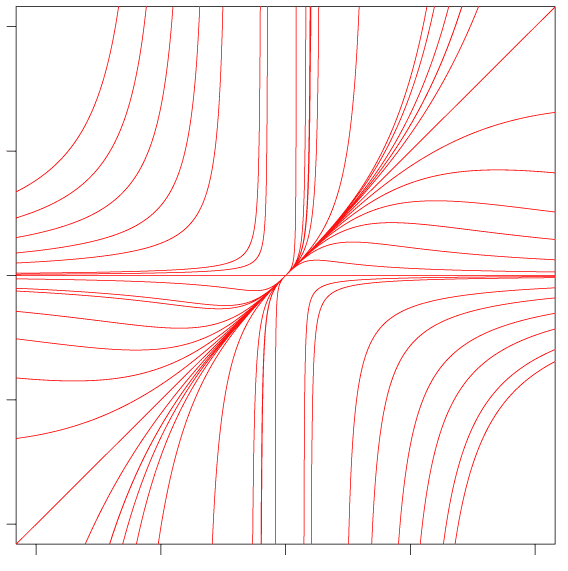
Итак, для изоклин \(y=0\) и \(y=x\) угол между изоклиной и интегральной кривой равен нулю. Как видно из графика, изоклины \(y=x\) в начале координат касается бесконечно много решений, изоклины \(y=0\) в начале координат не касается ни одно решение.
Приведем теперь строгое доказательство.
Пусть \(\dfrac{y}{x}=u\), тогда: \(y=u x\), \( y^{\prime}=x u^{\prime}+u\).
Уравнение \(y' = f(y/x)\) принимает вид:
\[x u^{\prime}+u=f(u)\]
Разделяя переменные получим:
\[\frac{d x}{x}=\frac{d u}{f(u)-u}\]
Учитывая, что \(k_0\) является корнем уравнения \(f(k) = k\), то в малой окресности начала координат имеем:
\[f(u)=f\left(k_{0}\right)+f^{\prime}\left(k_{0}\right)\left(u-k_{0}\right)+o\left(u-k_{0}\right)=k_{0}+f^{\prime}\left(k_{0}\right)\left(u-k_{0}\right)+o\left(u-k_{0}\right)\]
Следовательно:
\[\int_{k_{1}}^{u} \frac{d u}{f(u)-u}=\int_{k_{1}}^{u} \frac{d u}{k_{0}+f^{\prime}\left(k_{0}\right)\left(u-k_{0}\right)+o\left(u-k_{0}\right)-u}= \]
\[ =\int_{k_{1}}^{u} \frac{d u}{\left(f^{\prime}\left(k_{0}\right)-1\right)\left(u-k_{0}\right)+o\left(u-k_{0}\right)}\]
Проинтегрируем уравнение с разделенными переменными:
\[\int_{x_{1}}^{x} \frac{d x}{x}=\int_{k_{1}}^{k} \frac{d u}{f(u)-u}\]
Для левого интеграла получаем:
\[\int_{x_{1}}^{x} \frac{d x}{x}=\ln |x|-\ln \left|x_{1}\right|\]
Для правого интеграла получаем:
\[\int_{k_{1}}^{k} \frac{d u}{f(u)-u}=\frac{1}{f^{\prime}\left(k_{0}\right)-1}(\ln \left|u-k_{0}\right|-\ln \left|k_{1}-k_{0}\right|)\]
Рассмотрим теперь два случая:
1) \(f'(k_0)\lt 1\).
Тогда \(\ln |x|-\ln \left|x_{1}\right| \to-\infty\) при \(x \to 0\), а \( \ln \left|u-k_{0}\right|-\ln \left|k_{1}-k_{0}\right| \rightarrow-\infty\), при \(u \to k_{0}\).
Поскольку \(\dfrac{1}{f^{\prime}\left(k_{0}\right)-1}\lt1\), получаем:
\[\frac{1}{f^{\prime}\left(k_{0}\right)-1}\left(\ln \left|u-k_{0}\right|-\ln \left|k_{1}-k_{0}\right|\right) \rightarrow+\infty\]
Таким образом:
\[\begin{array}{l}{\int_{x_{1}}^{x} \frac{d x}{x} \to-\infty \text { при } x \to 0} \\ {\int_{k_{1}}^{u} \frac{d u}{f(u)-u} \to+\infty \text { при } u \to k_{0}}\end{array}\]
Равенство интегралов невозможно, следовательно никакая интегральная кривая не может касаться прямой \(y = k_0x\) в начале координат.
2) \(f'(k_0) \gt 1\).
Тогда:
\[\int_{k_{1}}^{u} \frac{d u}{f(u)-u} \to -\infty \text { при } u \to k_{0}\]
Cледовательно любая интегральная кривая касается прямой \(y = k_0x\) в начале координат.