Перевод книги "Обыкновенные дифференциальные уравнения и краевые задачи" Уильям Бойс, Ричард ДиПрима, Дуглас Мид ("Elementary Differential Equations and Boundary Value Problems" William E. Boyce, Richard C. DiPrima, Douglas B. Meade).

Глава 1: Введение

Раздел 1.1: Некоторые основные математические модели и поле направлений

Прежде чем приступить к серьезному изучению дифференциальных уравнений (например, с помощью этой книги), необходимо понять, чем это может быть полезно. Для некоторых студентов для мотивации хватит и внутренней заинтересованности к предмету, но для большинства будет важна возможность использовать дифференциальные уравнения в других областях науки.

Многие принципы или закономерности, лежащие в основе поведения мира природы, являются соотношениями или зависимостями, основанными на скорости изменения каких либо процессов. При переходе на язык математики, соотношения становятся уравнениями, а скорость изменения производной. Уравнения, в которые входит производная, называются дифференциальными уравнениями. Поэтому, чтобы понять и исследовать задачи связанные с движением жидкости, течением тока в электрических цепях, рассеянием тепла в твердых объектах, распространением сейсмических волн, или увеличением и сокращением популяций, помимо всего прочего, необходимо знать хоть что-нибудь о дифференциальных уравнениях.

Дифференциальное уравнение, которое описывает некоторый физический процесс, часто называют математическая моделью процесса, и многие такие модели будут рассматриваться на протяжении всей книги. В этом разделе мы начнем с двух моделей, приводящих к дифференциальным уравнениям которые легко решить. Интересно, что даже самые простые дифференциальные уравнения дают полезные модели важных физических процессов.

Пример 1. Падающий объект

Предположим, объект падает в атмосфере, на уровне моря. Необходимо составить дифференциальное уравнение, описывающее движение объекта.

Решение:

Мы начнем с обозначений различных величин, которые могут представлять интерес для этой задачи. Движение объекта происходит в течение некоторого промежутка времени, поэтому будем использовать \(t\) для обозначения времени. Далее, пусть \(v\) — это скорость движения объекта. Так как скорость изменяется со временем, то будем считать что \(v\) является функцией от \(t\). Другими словами, \(t\) — независимая переменная, \(v\) — зависимая от \(t\). В постановке задачи нет указаний по поводу единиц измерения, поэтому мы можем выбрать любые. Пусть время измеряется в секундах, скорость в метрах в секунду \((м/с)\). Далее мы будем предполагать, что вектор скорости направлен вниз, это так и есть, ведь объект падает.

Объект двигается в соответствии со вторым законом Ньютона, который говорит, что ускорение объекта, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе объекта. В математических терминах этот закон выражается уравнением

\[ F=ma,\tag*{(1)}\]

где \(m\) — масса объекта, \(a\) — ускорение, \(F\) — сила воздействующая на объект.

Чтобы наши единицы измерения оставались единообразными, мы будем измерять \(m\) в килограммах, \(a\) в метрах на секунду во второй степени \((м/с^2)\), \(F\) в ньютонах.

Конечно, \(a\) связано с \(v\):

\[a=\frac{dv}{dt}.\]

Так что мы можем переписать уравнение в виде:

\[F=m\frac{dv}{dt}.\tag*{(2)}\]

Далее, рассмотрим силы воздействующие на падающий объект. Сила тяжести — сила, действующая на любой физический объект, находящийся вблизи поверхности Земли, прямо пропорциональна массе объекта и равна \(mg\), где \(g\) — ускорение свободного падения. В выбранных нами единицах измерения, \(g\) примерно равно \(9.8 \ м/с^2\) рядом с поверхностью Земли.

Помимо силы тяжести на объект воздействует сила сопротивления воздуха. Мы не будем подробно останавливаться на этом моменте, достаточно будет сказать, что сила сопротивления пропорциональна скорости. Таким образом сила сопротивления равна \(\gamma v\), где \(\gamma\) это постоянная, называемая коэффициентом сопротивления. Величина коэффициента сопротивления зависит от физических параметров объекта, например гладкие и обтекаемые объекты имеют меньший коэффициент сопротивления чем шероховатые и не обтекаемые объекты. Единица измерения \(\gamma\) в данном случае \(кг/с\). Это может казаться странным, но не забывайте, \(\gamma v\) это сила сопротивления и она измеряется в \(кг\cdot м / с^2\).

Рис. 1.1.1. Силы, воздействующие на падающий объект.

Чтобы записать выражения для суммарной силы, нужно помнить что сила тяжести направлена вниз, а сила сопротивления, для падающих объектов, направлена вверх, как это изображено на рисунке 1.1.1. Таким образом:

\[F=mg-\gamma v.\tag*{(3)}\]

И мы получаем уравнение:

\[m\frac{dv}{dt}=mg-\gamma v.\tag*{(4)}\]

Полученное дифференциальное уравнение представляет собой математическую модель для скорости \(v\) объекта, падающего в атмосфере на уровне моря. Обратите внимание, что модель содержит три константы \(m\), \(g\) и \(\gamma\). Константы \(m\) и \(\gamma\) зависят от конкретного падающего объекта, и они различаются для разных предметов. Обычно их называют параметрами, поскольку они могут принимать разные значения в ходе эксперимента. С другой стороны, \(g\) является физической константой, значение которой одинаково для всех объектов.

Чтобы решить уравнение, нам нужно найти функцию \(v = v (t)\), которая удовлетворяет уравнению. Это не сложно, и мы покажем вам как это сделать в следующем разделе. А сейчас, посмотрим, что мы можем узнать о решениях уравнения, фактически не найдя ни одного из них. Наша задача будет проще, если мы присвоим числовые значения параметрам \(m\) и \(\gamma\) , но процедура исследования будет та же, независимо от того, какие значения мы выбираем. Итак, предположим, что \(m = 10 \ кг\) и \(\gamma = 2 \ кг/с\). Тогда уравнение можно переписать в виде:

\[\frac{dv}{dt}=9.8-\frac{v}{5}.\tag*{(5)}\]

Пример 2. Падающий объект (продолжение)

Исследовать поведение решений уравнения (5) без решения дифференциального уравнения.

Решение:

Для начала, рассмотрим, какую информацию можно получить непосредственно из самого дифференциального уравнения. Предположим, что у нас есть какое-то определенное заданное значение скорости \(v\). Зная это значение, из правой части уравнения (5) можно найти соответствующее значение \(dv / dt\). Например, если \(v = 40\), то \(dv / dt = 1.8\). Это значит, что наклон (угловой коэффициент) решения \(v = v (t)\) имеет значение \(1.8\) в любой точке, где \( v = 40\). Мы можем отобразить эту информацию графически в плоскости \(tv\), построив короткие отрезки с наклоном \(1.8\) в нескольких точках на прямой \(v = 40\) (Рисунок  1.1.2 (а)). Аналогично, если \(v = 50\), то \(dv / dt = −0.2\), если \(v = 60\), то \(dv / dt = −2.2\), поэтому мы строим отрезки с наклоном \(−0.2\) в нескольких точках линии \(v = 50\) (Рисунок 1.1.2 (б)) и отрезки с наклоном \(− 2.2\) в нескольких точках линии \(v = 60\) (Рисунок 1.1.2 (в)). Продолжая аналогично с другими значениями \(v\), мы построим так называемое поле направлений. Поле направлений для дифференциального уравнения (5) показано на рисунке 1.1.3.

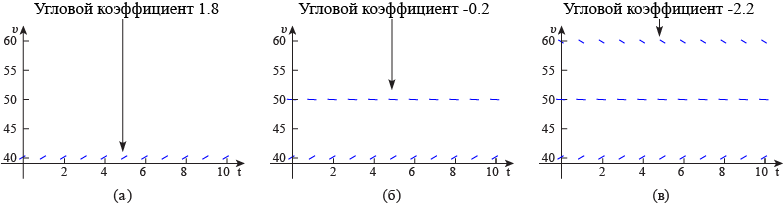
Рис. 1.1.2. Построение поля направлений для уравнения (5): \(dv/dt=9.8−v/5\). (а) \(v=40\), \(dv/dt=1.8\), (б) \(v=50\), \(dv/dt=−0.2\), (в) \(v=60\), \(dv/dt=−2.2\).

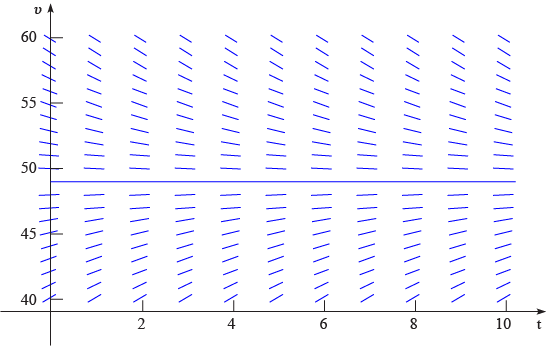
Рис. 1.1.3. Поле направлений и равновесное решение для уравнения (5): \(dv/dt=9.8−v/5\).

Как мы уже знаем, решением уравнения является функция \(v = v (t)\), график которой представляет собой кривую в плоскости \(tv\). Каждый отрезок на поле направлений является отрезком касательной к одному из решений уравнения. Таким образом, хотя мы не нашли ни одного решения, ни построили его график, тем не менее, мы можем сделать некоторые выводы о поведении решений. Например, если значение \(v\) меньше определенного переломного значения, то все отрезки имеют положительные наклоны, и скорость падающего объекта увеличивается по мере его падения. С другой стороны, если \(v\) больше переломного значения, то отрезки имеют отрицательные наклоны, а падающий объект замедляется. Что это за переломное значение \(v\), которое разделяет объекты, скорость которых увеличивается от тех, чья скорость уменьшается? Вернувшись к уравнению, мы можем найти значение \(v\), при котором \(dv / dt\) равно нулю. Это значение: \(v = 5 \cdot 9.8 = 49 \ м / с\).

Фактически, постоянная функция \(v(t) = 49\) является решением уравнения (5). Чтобы проверить это утверждение, подставим \(v(t) = 49\) в уравнение и заметим, что каждая сторона уравнения будет равна нулю. Поскольку решение \(v (t) = 49\) не меняется со временем, оно называется равновесным решением. В данном случае это решение, которое соответствует идеальному балансу между силой тяжести и силой сопротивления. На рисунке 1.1.3 видно, что равновесное решение \(v (t) = 49\) накладывается на поле направлений. Анализируя поле направлений, можно сделать еще один вывод: похоже, что все другие решения сходятся к равновесному решению по мере роста \(t\). В нашем случае, равновесное решение соответствует предельной скорости падения.

Подход, проиллюстрированный в Примере 2, может быть аналогично применен к более общему дифференциальному уравнению \((4)\), где параметры \(m\) и \(\gamma\) имеют неопределенные положительные значения. Результаты анализа по своей сути не отличаются от результатов Примера 2. Равновесное решение уравнения \((4)\) это постоянное решение \(v (t) = mg / \gamma\). Решения ниже равновесного решения растут со временем, те, что выше равновесного решения, убывают со временем. Соответственно, мы так же заключаем, что все решения приближаются к равновесному решению по мере роста \(t\).

Поле направлений

Поле направлений это очень удобный инструмент для исследования дифференциальных уравнений вида

\[\frac{dy}{dt}=f(t,y), \tag*{(6)}\]

где \(f\) - функция двух переменных \(t\) и \(y\). Поле направлений для уравнений вида (6) может быть построено путем вычисления \(f\) в каждой точке прямоугольной сетки. В каждой точке сетки строится короткий отрезок, наклон (угловой коэффициент) которого равен значению \(f\) в этой точке. Таким образом, каждый отрезок касается графика решения, проходящего через эту точку. Поле направлений, построенное на довольно плотной сетке, дает хорошую картину общего поведения решений дифференциального уравнения. Обычно сетки состоящей из нескольких сотен точек, вполне достаточно. Построение поля направлений почти всегда бывает очень полезно в качестве первого шага в исследовании дифференциального уравнения.

Отметим два вполне очевидных факта. Во-первых, для построения поля направления не нужно решать уравнение, достаточно рассчитать значение функции \(f(t,y)\) в точках некоторой прямоугольной сетки. Получается, поле направлений можно легко построить даже для уравнений, решение которых затруднено. Во-вторых, многократные повторные расчеты значений функции и построение отрезков формирующих поле направлений, это задачи хорошо решаемые с помощью компьютерный вычислений. Например, рисунки 1.1.2 и 1.1.3, были получены с помощью компьютера.

Полевые мыши и совы

Давайте теперь разберем немного другой пример. Рассмотрим некоторую популяцию полевых мышей, обитающих в некоторой сельской местности. В отсутствие хищников, мы предполагаем что популяция мышей увеличивается со скоростью, пропорциональной текущей популяции. Это предположение не является общепризнанным физическим законом (как закон движения Ньютона в Примере 1), но это вполне распространенная исходная гипотеза в исследовании роста популяции. Если мы обозначим время как \(t\), и размер популяция мышей в момент времени \(t\) как \(p(t)\), то предположение о росте популяции может быть выражено уравнением:

\[\frac{dp}{dt}=rp,\tag*{(7)}\]

где \(r\) - коэффициент пропорциональности, называемый скоростью роста.

Чтобы бы определиться с единицами измерениями, положим, что время измеряется в месяцах и коэффициент \(r\) равен \(0.5 / месяц\). Тогда оба выражения в уравнении (7) измеряются в \(мыши / месяц\).

Теперь предположим, что рядом с популяцией полевых мышей живет несколько сов, и они убивают 15 мышей в день (450 в месяц). Чтобы включить эту информацию в модель, мы должны изменить уравнение (7) следующим образом:

\[\frac{dp}{dt}=\frac{p}{2}-450.\tag*{(8)}\]

Пример 3. Рост популяции

Исследовать графически поведение решений уравнения (8).

Решение:

Поле направлений для уравнения (8) изображено на рисунке 1.1.4. Как видно из графика (и из уравнения (8)) при больших значения \(p,\) \(dp / dt\)  положительно и решения возрастают. Если \(p\) меньше определенной величины, то \(dp / dt\) отрицательно и решения убывают. Переломное значение, отделяющее возрастающие и убывающие решения, это значение \(p\) для которого \(dp / dt\) равно нулю. Приравняв нулю \(dp / dt\)  в уравнении (8), найдем равновесное решение \(p (t) = 900\), для которого скорость роста популяции мышей уравновешивается влиянием хищников. Равновесное решение также показано на рисунке 1.1.4.

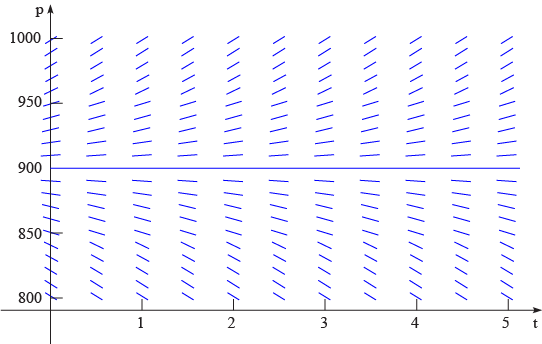
Рис. 1.1.4. Поле направлений и равновесное решение для уравнения (8): \(dp/dt=p/2−450\).

Сравнивая Примеры 2 и 3, отметим, что в обоих случаях равновесное решение разделяет возрастающие и убывающие решения. В Примере 2, все остальные решения сходятся (приближаются) к равновесному решению, и чем дольше падает объект, тем ближе его скорость к скорости равновесия. В Примере 3,  все остальные решения расходятся от равновесного решения. Решения ведут себя по-разному в зависимости от того, находятся они выше или ниже равновесного решения. Даже если некоторое решение изначально близко к равновесному, со временем величина популяции значительно отдалится от равновесного значения. В обеих задачах равновесное решение очень важно для понимания того, как ведут себя решения дифференциального уравнения.

Рассмотрим общую форму уравнения (8):

\[\frac{dp}{dt}=rp-k,\tag*{(9)}\]

где \(r\) - коэффициент скорости роста,  \(k\) - коэффициент влияния хищников. Поведение решений уравнения аналогично поведению решений уравнения (8). Равновесное решение уравнения (9): \(p (t) = k/r\). Решения выше равновесного решения возрастают, решения ниже равновесного решения убывают.

Следует помнить, что обе модели, обсуждаемые в этой главе, имеют свои ограничения. Модель падающего объекта (5) действительна только до тех пор, пока объект падает свободно, не встречая никаких препятствий. Если скорость достаточно велика, предположение о том, что сопротивление пропорционально скорости, должно быть заменено нелинейным приближением (см. задачу 21). Модель популяции (8) может уйти в отрицательную область \((p \lt 900)\) или достичь чрезвычайно больших значений \((p \gt 900)\). Оба варианта не реалистичны, такая модель становится неприемлемой через довольно короткий промежуток времени.

Построение математических моделей

При применении дифференциальных уравнений в исследовании процессов, необходимо сначала сформулировать соответствующее дифференциальное уравнение, которое описывает или моделирует исследуемую задачу. В этой главе мы рассмотрели два примера процесса моделирования, один из которых взят из физики, другой из экологии.

При создании математических моделей вы должны понимать, что каждая задача отличается, и что успешное моделирование не может быть сведено к следованию набора предписанных правил. Построение удовлетворительной модели иногда является самой сложная частью задачи.

Тем не менее, можно выделить определенные шаги, которые часто являются частью процесса:

1. Определите и обозначьте независимые и зависимые переменные. Часто независимой переменной является время.

2. Выберите единицы измерения для каждой переменной. В некоторых случаях, определенные единицы измерения могут быть намного удобнее, чем другие. Например, мы решили измерять время в секундах для задачи о падающем объекте и в месяцах для задачи роста популяции.

3. Сформулируйте основной принцип, лежащий в основе задачи которую вы исследуете. Это может быть известный физический закон, такой как закон Ньютона, или некоторое предположение, которое может быть основано на вашем собственном опыте или наблюдении. Этот шаг подразумевает, что вы знакомы с областью, с которой связана задача.

4. Выразите принцип из шага 3 в терминах переменных, которые были выбраны в первом шаге. Это не всегда просто сделать, может потребоваться введение физических констант или параметров (такие как коэффициент сопротивления в Примере 1) и определение соответствующих значений для них. Или это может включать использование вспомогательных или промежуточных переменных, которые связаны с первичными переменными.

5. Если единицы измерения в уравнении совпали, то, по крайней мере, ваше уравнение является согласованным по размерности. Но, уравнение может иметь и другие недостатки, которые этот тест не выявил.

6. В рассматриваемых в этой главе задачах результатом шага 4 является дифференциальное уравнение, которое описывает необходимую математическую модель. Но математическая модель может быть намного более сложной, например в виде системы из нескольких дифференциальных уравнений.

Историческая справка, часть I: Ньютон, Лейбниц и Бернулли

Не зная ничего о дифференциальных уравнениях и методах их решения сложно оценить историю этого важного раздела математики. Кроме того, развитие дифференциальных уравнений тесно связаны с общим развитием математики. Тем не менее, чтобы обеспечить историческую перспективу, мы приведем некоторые из основных тенденций в истории предмета и перечислим ученых, которые внесли большой вклад на раннем этапе развития дифференциальных уравнений. В текущем разделе мы рассмотрим исследования ученых семнадцатого века. Историческая справка будет продолжена в Разделе 1.2 с обзора вклада Эйлера и других математиков восемнадцатого (и начала девятнадцатого) века. Более поздние достижения, включая использование компьютеров и других технологий, будут приведены в конце Раздела 1.3. Дополнительная историческая информация содержится в сносках по всей книге и литературе, список которой приведен в конце этой главы.

Предмет дифференциальных уравнений возник при изучении математического анализа Исааком Ньютоном (1643-1727) и Готфридом Вильгельмом Лейбницем (1646-1716) в семнадцатом веке. Ньютон вырос в английской сельской местности, получил образование в Тринити-колледж (Колледж Святой Троицы) Кембриджского университета и в 1669 году был избран на должность «лукасовского профессора» математики и оптики Тринити-колледжа. Его эпохальные открытия в дифференциальном исчислении и основные законы механики датируются 1665 годом. Они были распространены в частном порядке среди его друзей, но Ньютон был чрезвычайно чувствителен к критике и не стал публиковать свои результаты до 1687 года, когда был опубликован один из самых знаменитых в истории науки трудов "Математические начала натуральной философии". Хотя Ньютон проделал относительно небольшую работу в дифференциальных уравнениях как таковых, его разработка математического анализа и исследование основных принципов механики стали основой для дальнейшего их развития в восемнадцатом веке. Ньютон выделил три формы дифференциала для уравнений первого порядка: \(dy / dx = f (x)\), \(dy / dx = f (y)\), и \(dy / dx = f (x, y)\). Для последнего уравнения он разработал метод решения с использованием бесконечных рядов, в случае когда \(f (x, y)\) является полиномом от \(x\) и \(y\).  Активные исследования Ньютона по математике закончились в начале 1690-х годов, за исключением решения редких «проблемных задач» и пересмотра и публикации результатов, полученных много ранее. Он был назначен был назначен мастером Британского Монетного двора в 1696 году и несколько лет спустя оставил свою должность профессора. В 1705 году он был посвящен в рыцари и после его смерти в 1727 году стал первым ученым, который был похоронен в Вестминстерском аббатстве.

Лейбниц родился в 1646 году в Лейпциге, Германия. В 1663 году Лейбниц опубликовал свой первый трактат «О принципе индивидуации» и получил степень бакалавра, а в 1664 году получил степень магистра философии. В 1666 году (в возрасте 20 лет) получил степень доктора права в Альтдорфском университете в Альтдорф-Нюрнберге. На протяжении всей своей жизни он занимался научной работой в нескольких различных направлениях. Он был в основном самоучкой в математике, так как его интерес к этому предмету появился когда ему было за двадцать. Лейбниц пришел к фундаментальным результатам математического анализа независимо, хотя немного позже, чем Ньютон, но был первым, кто опубликовал их в 1684 году. Лейбниц очень хорошо понимал силу математических обозначений и именно он ввел обозначение \(dy/dx\) для производной и знак интеграла. Он открыл метод разделения переменных (Раздел 2.2) в 1691 году, приведение однородных уравнений к уравнениям с разделяющимися переменными (Раздел 2.2, Задача 30) в 1691 году и метод решения линейных уравнений первого порядка (Раздел 2.1) в 1694 году. Часть своей жизни Лейбниц провел на службе у королевских семей в качестве советника, историка, библиотекаря и дипломата, что позволило ему много путешествовать и вести обширную переписку с другими математиками, особенно братьями Бернулли. Во многом благодаря этому, многие задачи в дифференциальных уравнениях были разрешены в конце семнадцатого века.

Братья Бернулли, Якоб (1654-1705) и Иоганн (1667-1748), из Базеля (Швейцария), сделали очень много для разработки методов решения дифференциальных уравнений и расширения областей их применения. Якоб стал профессором математики в Базеле в 1687 году, и Иоганн был назначен на ту же должность после смерти своего брата в 1705 году. Оба брата были раздражительны, ревнивы и часто ввязывались в споры, особенно друг с другом. Тем не менее, оба также внесли значительный вклад в несколько областей математики. С помощью математического анализа они решили ряд проблем механики, сформулировав их как дифференциальные уравнения. Например, Якоб Бернулли решил дифференциальное уравнение \(y^{\prime}=\left(a^{3} /\left(b^{2} y-a^{3}\right)\right)^{1 / 2}\)  (Задача 9 в Разделе 2.2) в 1690 году и в той же статье впервые использовал термин «интеграл» в современном смысле. В 1694 году Иоганн Бернулли решил уравнение \(dy/ dx = y / (ax)\) (Задача 10 в Разделе 2.2). Одной из задач, которую решили оба брата, была задача о брахистохроне, и это привело к большому разногласию между ними. Задача о брахистохроне была также решена Лейбницем, Ньютоном и Лопиталем. По рассказам его племянницы Ньютона, Ньютона узнал о задаче, в четыре часа дня, когда усталый вернулся из Монетного двора и спустя 12 часов решение было готово. Он опубликовал решение анонимно, но, увидев простое решение этой задачи, содержавшее всего 77 слов, Иоганн Бернулли угадал автора, он сказал: «Tanquam ex ungue leonem» — «По когтям узнают льва».

Даниил Бернулли (1700-1782), сын Иоганна, в 1721 году сдал экзамены на медика в Базеле, защитил диссертацию. В 1724 году выпустил «Математические этюды», принёсшие ему известность. В 1725 год переехал в Петербург в Петербургскую академию наук, где занимался вначале медициной, затем математикой. В 1733 году вернулся в Базель, где стал  профессором ботаники, а затем физики. Областью его интересов были в основном дифференциальные уравнения в частных производных и их приложения. Например, именно с его именем связано уравнение Бернулли в механике жидкости. Он также был первым, кто исследовал функции, которые столетие спустя будут известны как функции Бесселя (Раздел 5.7).