В прямоугольный бак размером \(60 \ см\) x \(75 \ см\) и высотой \(80 \ см\) поступает \(1,8 \ л\) воды в секунду. В дне имеется отверстие площадью \(2,5 \ см^2.\) За какое время наполнится бак? Сравнить результат с временем наполнения такого бака без отверстия в дне. Жидкость из сосуда вытекает со скоростью, равной \(0,6\sqrt{2gh}\), где \(g = 10 \ м/сек^2\) — ускорение силы тяжести, \(h\) — высота уровня воды над отверстием.
Решение
Пусть \(h(t)\) - высота уровня воды в баке над отверстием в момент времени \(t\). Через промежуток времени \(\Delta t\) уровень воды изменится до \(h(t+\Delta t)\).
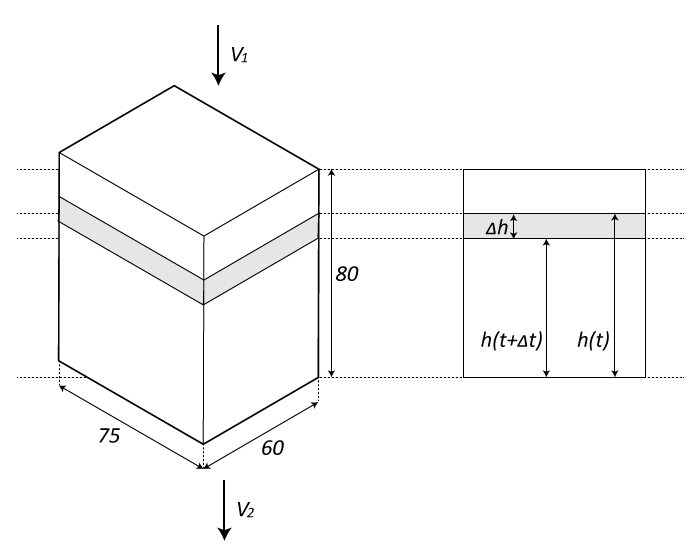
Изменение объема воды в баке за время \(\Delta t\):
\[\Delta V=\Delta h \cdot 60 \cdot 75,\]
где \(\Delta h = h(t+\Delta h)-h(t).\)
Изменение объема происходит за счет поступления воды \(\Delta V_1\) и утечки через отверстие \(\Delta V_2\).
Так как поступает \(1,8 \ л\) воды в секунду (или \(1800см^3\) воды в секунду), то:
\[\Delta V_1=1800 \Delta t.\]
Объем вытекающей воды:
\[\Delta V_2=2,5 \cdot 0,6\sqrt{2gh(t)}\Delta t.\]
Так как \(\Delta V=\Delta V_1-\Delta V_2,\) то:
\[\Delta h \cdot 60 \cdot 75=1800 \Delta t-2,5 \cdot 0,6\sqrt{2gh(t)}\Delta t\]
Разделив на \(\Delta t\), совершив предельный переход при \(\Delta t \to 0\) и подставив \(g = 10 \ м/сек^2 = 1000 \ см/сек^2,\) получим:
\[4500\frac{dh}{dt}=1800-1,5\sqrt{2gh}\]
Это уравнение с разделяющимися переменными. Разделим переменные:
\[\frac{1}{1800-1,5\sqrt{2gh}}dh=\frac{1}{4500} dt\]
Или:
\[\frac{1}{1200-\sqrt{2gh}}dh=\frac{1}{3000} dt\]
Интегрируем:
\[\int\frac{1}{1200-\sqrt{2gh}}dh=\int\frac{1}{3000} dt\]
Рассмотрим левый интеграл:
\[\int \frac{1}{1200-\sqrt{2gh}}dh=\frac{2}{\sqrt{2g}}\int \frac{\sqrt{h}}{1200-\sqrt{2gh}}d(\sqrt{2gh})=\]
\[=\frac{2}{(\sqrt{2g})^2}\int \frac{\sqrt{2gh}}{1200-\sqrt{2gh}}d(\sqrt{2gh})=\]
\[=\frac{2}{(\sqrt{2g})^2}\int \frac{\sqrt{2gh}+1200-1200}{1200-\sqrt{2gh}}d(\sqrt{2gh})=\]
\[=-\frac{2}{(\sqrt{2g})^2}\int d(\sqrt{2gh}) -1200\frac{2}{(\sqrt{2g})^2}\int\frac{1}{1200-\sqrt{2gh}}d(\sqrt{2gh})=\]
\[=-\frac{2\sqrt{h}}{\sqrt{2g}} -\frac{1200}{g}\ln(1200-\sqrt{2gh})+C\]
Получаем решение:
\[\frac{t}{3000}=-\frac{2\sqrt{h}}{\sqrt{2g}} -\frac{1200}{g}\ln(1200-\sqrt{2gh})+C\]
Так как в момент времени \(t=0\) бак пустой, то \(h(0)=0.\) Получаем \(C=1,2\ln1200\).
Чтобы найти время, за которое наполнится бак, подставим в уравнение \(h=80\):
\[\frac{t}{3000}=-\frac{2\sqrt{80}}{\sqrt{2000}} -1,2\ln(800)+1,2\ln1200\]
\[\frac{t}{3000}\approx 0.0865\]
\[t\approx 259.6743891\]
Получаем, бак заполнится за 260 секунд.
В случае, если отверстие в дне отсутствует, то \(\Delta V=\Delta V_1,\) и уравнение принимает вид:
\[4500\frac{dh}{dt}=1800\]
Решение уравнения:
\[2,5h=t+C\]
Так как в момент времени \(t=0\) бак пустой, то \(h(0)=0.\) Получаем \(C=0\).
Чтобы найти время, за которое наполнится бак, подставим в уравнение \(h=80\): \(t=2,5 \cdot 80=200\).
Получаем, без отверстия в дне, бак заполнится за 200 секунд.