Найти кривые, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная \(a^2\).
Решение
Схематично построим треугольник в двух вариантах (для положительной и отрицательной \(y'\)):
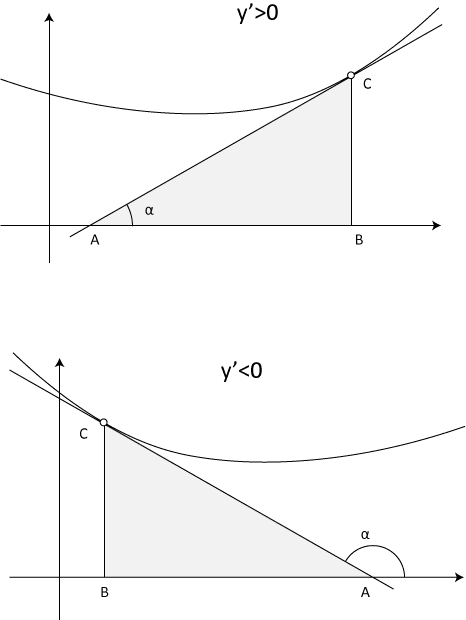
Рассмотрим вначале \(y' \gt 0 \). Площадь прямоугольного треугольника:
\[S=\frac{1}{2}AB \cdot BC\]
Выразим \(AB\) через \(BC\): \(BC=AB \cdot \tan \alpha\).
\[AB=\frac{BC}{\tan \alpha}\]
Так как \(BC=y\) и \(\tan \alpha=y'\) получаем:
\[S=\frac{y^2}{2y'}\]
Подставив начальное условие на площадь, получим дифференциальное уравнение:
\[2y'a^2=y^2.\]
Найдем решение. Это уравнение является уравнением с разделяющимися переменными. Разделим переменные:
\[\frac{2a^2}{y^2}dy=dx\]
Переменные разделены. Интегрируем обе части уравнения:
\[-\frac{2a^2}{y}=x+C\]
\[y=-\frac{2a^2}{x+C}\]
Таким образом, уравнения семейства кривых для \(y' \gt 0\) имеет вид:
\[y=-\frac{2a^2}{x+C}\]
Если \(y' \lt 0\), то \(BC=AB \cdot \tan (180^o-\alpha)=-AB \cdot \tan \alpha\). Соответственно:
\[S=-\frac{y^2}{2y'}\]
Дифференциальное уравнение имеет вид:
\[2y'a^2=-y^2.\]
Разделяя переменные и интегрируя получим решение:
\[y=-\frac{2a^2}{-x+C}\]
Таким образом, уравнения семейства кривых для \(y' \lt 0\) имеет вид:
\[y=-\frac{2a^2}{-x+C}\]
Объединяя, получим уравнение кривых:
\[y=-\frac{2a^2}{\pm x+C}.\]