C помощью изоклин начертить (приближенно) решения уравнения \(y'+y=(x-y')^3\).
Решение
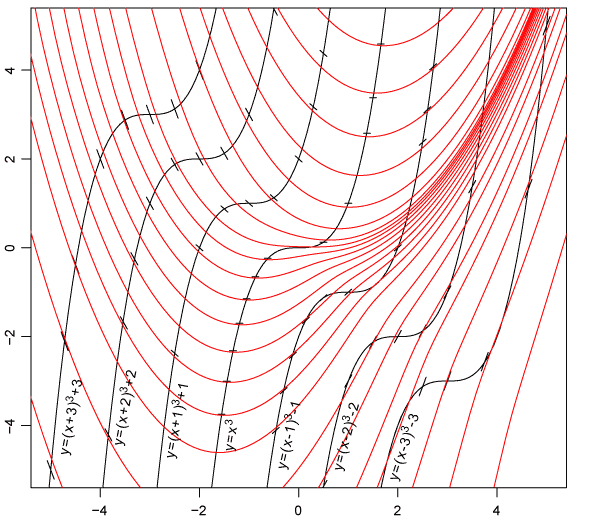
Для получения уравнения изоклин положим \(y′=const=k\), тогда общее уравнение изоклин имеет вид: \(y=(x-k)^3-k\).
Изоклинами являются кубические параболы. Построим изоклины для значений \(k\) равных \(-3,-2,-1,0,1,2,3\) , отметим направления задаваемые параметром \(k\) и построим решения: