Задача 64. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям

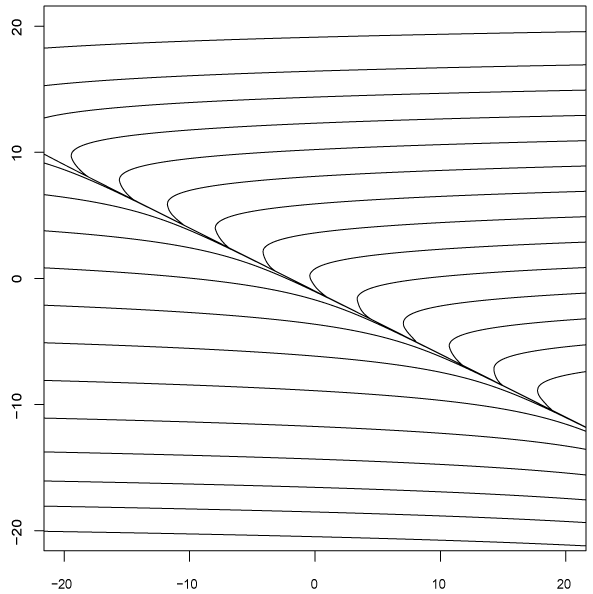
Решить уравнение и построить несколько интегральных кривых: $(x+2y)y^{\prime }=1$. Найти решения, удовлетворяющие начальным условиям: $y(0)=-1$.

Решение
Введем замену: $z=x+2y$.
$$z^{\prime }=1+2y^{\prime }\Rightarrow y^{\prime }=\frac{z^{\prime }-1}{2}$$
Получаем:
$$z\frac{z^{\prime }-1}{2}=1$$
Это уравнение является уравнением с разделяющимися переменными. Разделим переменные:
$$z^{\prime }=\frac{2}{z}+1$$
$$z^{\prime }=\frac{2+z}{z}$$
$$\frac{z}{2+z}dz=dx$$
Переменные разделены. Интегрируем обе части уравнения:
$$\int \frac{z}{2+z}dz=\int dx$$
$$\int \frac{z}{2+z}dz=\int dz-\int \frac{2}{2+z}dz=z-2\ln |2+z|+C$$
Получаем:
$$z-2\ln |2+z|=x+C$$
Проведем обратную замену:
$$x+2y-2\ln |2+x+2y|=x+C$$
$$2\ln |2+x+2y|=2y+C$$
$$2+x+2y=C_1{e}^y$$

При делении на $z+2$ могло быть потеряно решение $x+2y+2=0$. Решение $x+2y+2=0$ входит в общее решение при $C_1=0$.

Таким образом, решение уравнения:
$$2+x+2y=C_1{e}^y.$$

Найдем решение для условия $y(0)=-1$. Подставим условие в общее уравнение:
$$2+0-2=C_1{e}^{-1}\Rightarrow C_1=0.$$
Получаем решение: $2+x+2y=0$.

Интегральные кривые: