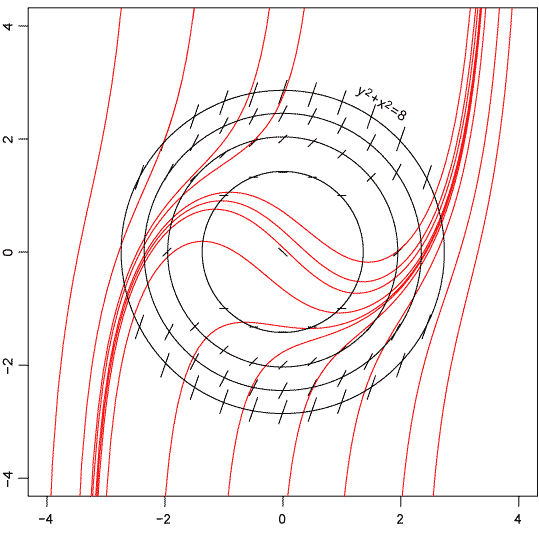
C помощью изоклин начертить (приближенно) решения уравнения \(y'=\frac{x^2+y^2}{2}-1\).
Решение
Для получения уравнения изоклин положим \(y′=const=k\), тогда \(y^2+x^2=2k+2\) или \(y=\pm \sqrt{2k+2-x^2}\), где \(k\ge-1\).
Изоклинами являются окружности с центром в точке \((0,0)\). При \(k=-1\) окружность вырождается в точку. При возрастании \(k\), растет радиус окружностей, и касательная к интегральным кривым становится более вертикальной.
Построим семейство окружностей для значений \(k\) равных \( 0,1,2, 3\) , отметим направления задаваемые параметром \(k\) и построим решения: