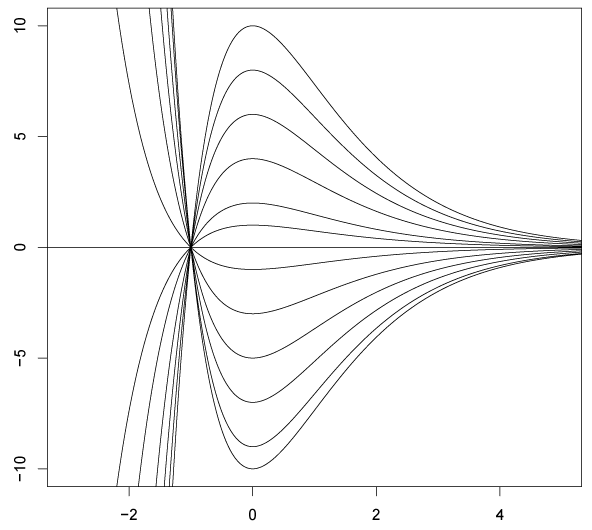
Решить уравнение и построить несколько интегральных кривых: \(xy \ dx+(x+1)\ dy=0\).
Решение
Это уравнение является уравнением с разделяющимися переменными. Разделим переменные:
\[ xy \ dx=-(x+1)\ dy\]
\[ \frac{x}{(x+1)}dx=-\frac{1}{y}dy\]
Переменные разделены. Интегрируем обе части уравнения:
\[ \int \frac{x}{(x+1)}dx=-\int\frac{1}{y}dy\]
\[ \int \frac{x+1-1}{(x+1)}dx=-\int\frac{1}{y}dy\]
\[ \int dx-\int\frac{1}{(x+1)}dx=-\int\frac{1}{y}dy\]
Получаем:
\[x-\ln|x+1|=-\ln|y| +\ln|C|.\]
Или:
\[\ln|y|=\ln|x+1|-x+\ln|C|=\ln|x+1|-\ln|e^x|+\ln|C|=\ln|\frac{x+1}{e^x }C|.\]
Тогда:
\[y=\frac{x+1}{e^x}C\]
При делении на \(y(x+1)\) могли быть потеряны решения \(y = 0\) и \(x =-1\). Решение \(y = 0\) входит в общее решение уравнения при \(C=0\); \(x=-1\) является решением уравнения.
Ответ: \(y=(x+1)e^{-x}C; x=-1\).
Интегральные кривые: