геометрические и физические задачи

Найти кривую, у которой точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат.

Решение
Построим график в соответствии с условиями:

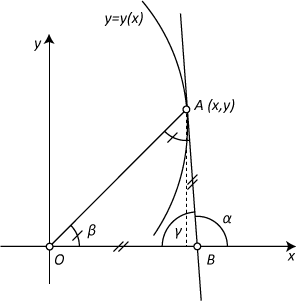
Точка $B$ является точкой пересечения касательной и оси абсцисс. Поскольку она одинаково удалена от точки касания и от начала координат, получаем:
$$|OB|=|BA|$$
Треугольник OBA является равнобедренным и $\gamma ={180}^o-2\beta$. Соответственно:
$$\alpha ={180}^o-\gamma =2\beta$$
Получаем:
$$\text{tg}\alpha =\text{tg}2\beta =\frac{2\text{tg}\beta }{1-{\text{tg}}^2\beta }$$
Учитывая что $\text{tg}\beta ={\displaystyle \frac{y}{x}}$, получаем:
$$\text{tg}\alpha =\frac{2{\displaystyle \frac{y}{x}}}{1-{\displaystyle \frac{y^2}{x^2}}}$$
$$\text{tg}\alpha =\frac{2xy}{x^2-y^2}$$
Таким образом, учитывая геометрический смысл производной, получаем дифференциальное уравнение кривой:
$$y^{\prime }=\frac{2xy}{x^2-y^2}$$
Уравнение является однородным.
Проведем замену $y=tx$:
Найдем производную:
$$\frac{dy}{dx}=t+x\frac{dt}{dx}$$
Подставим замену и полученную производную в уравнение:
$$t+x\frac{dt}{dx}=\frac{2t}{1-t^2}$$
$$x\frac{dt}{dx}=\frac{2t}{1-t^2}-t$$
$$x\frac{dt}{dx}=\frac{2t-t+t^3}{1-t^2}$$
$$x\frac{dt}{dx}=\frac{t(1+t^2)}{1-t^2}$$
Это уравнение является уравнением с разделяющимися переменными. Разделим переменные:
$$\frac{1-t^2}{t(1+t^2)}dt=\frac{1}{x}dx$$
Переменные разделены. Интегрируем обе части уравнения:
$$\int \frac{1-t^2}{t(1+t^2)}dt=\int \frac{1}{x}dx$$
Рассмотрим левый интеграл. Преобразуем дробь:
$$\frac{1-t^2}{t(1+t^2)}=\frac{1}{t(1+t^2)}-\frac{t}{1+t^2}=\frac{1+t^2-t^2}{t(1+t^2)}-\frac{t}{1+t^2}=\frac{1}{t}-2\frac{t}{1+t^2}$$
Получаем:
$$\int \frac{1}{t}dt-2\int \frac{t}{1+t^2}dt=\int \frac{1}{x}dx$$
$$\int \frac{1}{t}dt-\int \frac{d(1+t^2)}{1+t^2}=\int \frac{1}{x}dx$$
$$\ln |t|-\ln |1+t^2|=\ln Cx$$
$$\frac{t}{1+t^2}=Cx$$
Произведем обратную замену. Так как $y=tx$, получаем:
$$\frac{{\displaystyle \frac{y}{x}}}{1+{\displaystyle \frac{y^2}{x^2}}}=Cx$$
$$\frac{yx}{x^2+y^2}=Cx$$
$$y=C(x^2+y^2)$$
Таким образом, мы получили уравнение кривой, у которой точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат:
$$y=C(x^2+y^2).$$