Воронка имеет форму конуса радиуса \(R = 6 \ см\) и высоты \(H= 10 \ см\), обращенного вершиной вниз. За какое время вытечет вся вода из воронки через круглое отверстие диаметра \(0,5 \ см\), сделанное в вершине конуса? Жидкость из сосуда вытекает со скоростью, равной \(0,6\sqrt{2gh}\), где \(g = 10 \ м/сек^2\) — ускорение силы тяжести, \(h\) — высота уровня воды над отверстием.
Решение
Пусть \(h(t)\) - высота уровня воды в воронке над отверстием в момент времени \(t\). Через промежуток времени \(\Delta t\) уровень воды понизится до \(h(t+\Delta t)\). При бесконечно малых \(\Delta t\), объем воды вытекшей из воронки за это время можно принять равным: \(V_1=-\pi r_1^2 \Delta h, \) где \(\Delta h = h(t+\Delta h)-h(t).\)
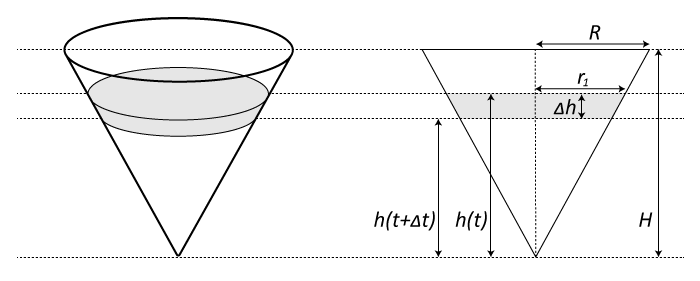
С другой стороны, объем воды вытекающей из отверстия в вершине конуса равен:
\[V_2=\pi r_2^2 0,6\sqrt{2gh}\Delta t\]
Поскольку эти объемы равны:
\[-\pi r_1^2 \Delta h=\pi r_2^2 0,6\sqrt{2gh}\Delta t\]
Получаем дифференциальное уравнение:
\[ -r_1^2 \frac{dh}{dt}= r_2^2 0,6\sqrt{2gh}\]
Здесь \(r_2=0,25 \ см\) это константа из условия, а \(r_1\) можно найти из соотношения (следующего из подобия треугольников):
\[\frac{R}{H}=\frac{r_1}{h(t)} \Rightarrow r_1=\frac{h(t)R}{H}.\]
Таким образом, уравнение имеет вид:
\[- \frac{h^2R^2}{H^2} \frac{dh}{dt}= r_2^2 0,6\sqrt{2gh}\]
Преобразуем:
\[h\sqrt{h} dh+\frac{H^2r_2^2}{R^2}0,6 \sqrt{2g}dt=0\]
Введем обозначение \(K\) и подставим значения из условия \(R = 6 \ см=0,06 \ м;\) \(H= 10 \ см=0,1 \ м;\) \(r_2=0,25 \ см=0,0025 \ м\):
\[K=\frac{H^2r_2^2}{R^2}0,6 \sqrt{2g}=\frac{0,1^2 \cdot 0,0025^2}{0,06^2}0,6 \sqrt{2 \cdot 10}\approx 0,0000466\]
Получаем:
\[h^{\frac{3}{2}}dh+Kdt=0\]
Это уравнение с разделяющимися переменными. Интегрируя, получаем:
\[\int h^{\frac{3}{2}}dh+K\int dt=0\]
Получаем общее решение:
\[\frac{2}{5} h^{\frac{5}{2}}+Kt=C\]
Так как в момент времени \(t=0,\) \(h(0)=H,\) получаем:
\[C=\frac{2}{5} H^{\frac{5}{2}} \approx 0,0012649\]
Окончательно получаем уравнение:
\[\frac{2}{5} h^{\frac{5}{2}}+0,0000466t=0,0012649\]
Для нахождения времени, за которое вся вода вытечет из воронки, подставим \(h=0\), и получим:
\[t=\frac{0,0012649}{0,0000466}\approx 27,153\]
Таким образом, вся вода вытечет через 27 секунд.