Задача 12. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям

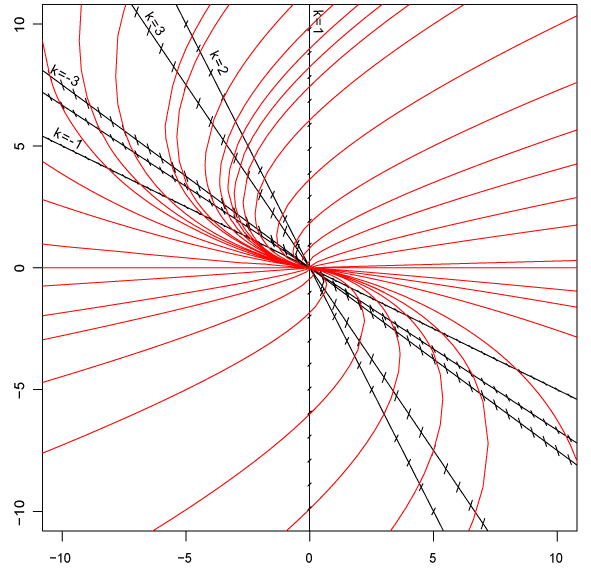
C помощью изоклин начертить (приближенно) решения уравнения $y^{\prime }=\frac{y}{x+y}$.

Решение
Для получения уравнения изоклин положим $y\prime =const=k$, тогда:
$$k=\frac{y}{x+y}$$
$$k(x+y)=y$$
$$kx=y-yk$$
$$y=x\frac{k}{1-k}$$
Изоклинами являются прямые, проходящие через начало координат. При $k=0$, уравнение изоклины имеет вид $y=0$, эта изоклина является решением исходного уравнения. При $k=1$, уравнение изоклины имеет вид $x=0$.

Построим изоклины для значений $k$ равных $-3,-2,-1,0,1,2,3$, отметим направления задаваемые параметром $k$ и построим решения: