Задача 173. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям

Найти кривые, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная $3a^2$.

Решение
Схематично изобразим трапецию:

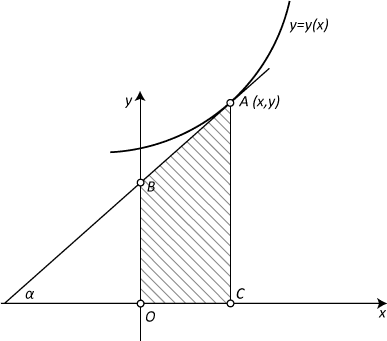
$A$ - точка касания; $OBAC$ - трапеция ограниченная осями координат, касательной и ординатой точки касания.

Площадь трапеции $OBAC$:
$$S=\frac{|OB|+|CA|}{2}|OC|$$
Поскольку $|CA|=y$, а $|OC|=x$, осталось найти $|OB|$.

Уравнение касательной в точке $A$: $y=y_A+y_A^{\prime }(x-x_A)$
Поскольку касательная проходит через точку $B$, получаем:
$$y_B=y_A+y_A^{\prime }(x_B-x_A)$$
Соответственно, так как $x_B=0$ и точка $A$ имеет координаты $(x,y)$, получаем:
$$|OB|=y_B=y-y^{\prime }x$$
Таким образом:
$$S=\frac{|OB|+|CA|}{2}|OC|=\frac{y-y^{\prime }x+y}{2}x=\frac{2y-y^{\prime }x}{2}x$$

Так как по условию площадь трапеции равна $3a^2$, получаем уравнение семейства кривых:
$$y^{\prime }-\frac{2y}{x}=-\frac{6a^2}{x^2}$$

Данное уравнение является линейным дифференциальным уравнением.
Найдем решение однородного уравнения:
$$y^{\prime }-\frac{2y}{x}=0$$
Разделим переменные:
$$\frac{dy}{y}=2\frac{dx}{x}$$
Переменные разделены. Интегрируем обе части уравнения:
$$\int \frac{dy}{y}=2\int \frac{dx}{x}$$
$$\ln |y|=2\ln |x|+\ln C$$
$$y=C{x}^2$$

Таким образом, решение однородного уравнения: $y=C{x}^2$.
Считая постоянную $C$ функцией от $x$, подставим решение однородного уравнения в исходное уравнение.
Так как $y^{\prime }=C^{\prime }{x}^2+2Cx$, то:
$$C^{\prime }{x}^2+2Cx-\frac{2C{x}^2}{x}=-\frac{6a^2}{x^2}$$
$$C^{\prime }{x}^2=-\frac{6a^2}{x^2}$$
$$C^{\prime }=-\frac{6a^2}{x^4}$$
$$C=-\int \frac{6a^2}{x^4}dx=\frac{6a^2}{3x^3}+C_1$$

Подставим полученную функцию в решение однородного уравнения:
$$y=C{x}^2=(\frac{6a^2}{3x^3}+C_1)x^2=\frac{2a^2}{x}+C_1{x}^2$$

Таким образом, уравнение семейства кривых, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная $3a^2$:
$$y=\frac{2a^2}{x}+C_1{x}^2.$$