Задача 134. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям

Пусть $k_0$ — корень уравнения $f(k)=k$. Показать, что:
1) если $f^{\prime }(k_0)<1$, то ни одно решение уравнения $y^{\prime }=f(y/x)$ не касается прямой $y=k_{0}x$ в начале координат;
2) если $f^{\prime }(k_0)>1$, то этой прямой касается бесконечно много решений.

Решение
Для начала рассмотрим геометрическую интерпретацию задачи.

Уравнение $y^{\prime }=f(y/x)$ является однородным дифференциальным уравнением. Изоклины уравнения имеют вид $f(y/x)=k$, где $k$ - постоянная.

Получаем, что изоклинами однородного дифференциального уравнения являются прямые проходящие через начало координат $y=ax$, где $a=f^{-1}(k)$.

Тангенс угла между прямой $y=ax$ и пересекающей его интегральной кривой уравнения $y^{\prime }=f(y/x)$ равен $(f(a)-a)/(1+af(a))$, соответственно если $k_0$ — корень уравнения $f(k)=k$, то $y=k_{0}x$ это изоклина для которой угол между ней и интегральными кривыми равен нулю.

Рассмотрим пример:
$$y^{\prime }=2\frac{y^2}{x^2}-\frac{y}{x}$$
$$f(k)=2k^2-k$$
Найдем решение уравнения $f(k)=k$:
$$2k^2-k=k\Rightarrow k(k-1)=0\Rightarrow k_0=0;k_0=1$$
Найдем $f^{\prime }(k_0)$:
$$f(k)=2k^2-k\Rightarrow f^{\prime }(k)=4k-1$$
Получаем: $f^{\prime }(0)=-1$ и $f^{\prime }(1)=3$.
Построим приближенно интегральные кривые:

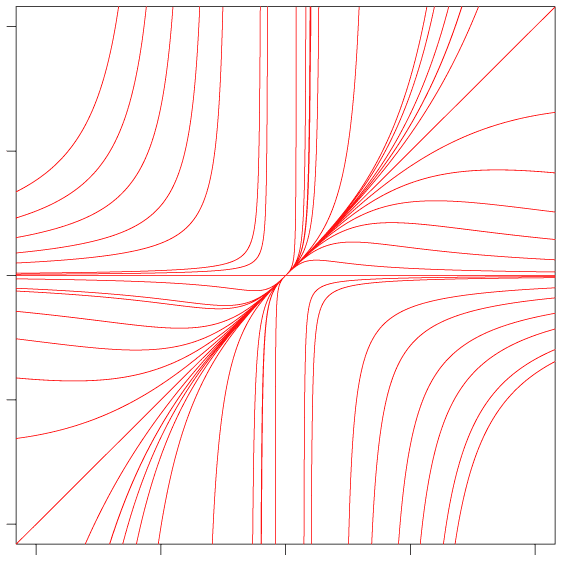
Итак, для изоклин $y=0$ и $y=x$ угол между изоклиной и интегральной кривой равен нулю. Как видно из графика, изоклины $y=x$ в начале координат касается бесконечно много решений, изоклины $y=0$ в начале координат не касается ни одно решение.

Приведем теперь строгое доказательство.

Пусть ${\displaystyle \frac{y}{x}}=u$, тогда: $y=ux$, $y^{\prime }=x{u}^{\prime }+u$.
Уравнение $y^{\prime }=f(y/x)$ принимает вид:
$$x{u}^{\prime }+u=f(u)$$
Разделяя переменные получим:
$$\frac{dx}{x}=\frac{du}{f(u)-u}$$
Учитывая, что $k_0$ является корнем уравнения $f(k)=k$, то в малой окресности начала координат имеем:
$$f(u)=f\left(k_0\right)+f^{\prime }\left(k_0\right)(u-k_0)+o(u-k_0)=k_0+f^{\prime }\left(k_0\right)(u-k_0)+o(u-k_0)$$
Следовательно:
$${\int }_{k_1}^u\frac{du}{f(u)-u}={\int }_{k_1}^u\frac{du}{k_0+f^{\prime }\left(k_0\right)(u-k_0)+o(u-k_0)-u}=$$

$$={\int }_{k_1}^u\frac{du}{(f^{\prime }\left(k_0\right)-1)(u-k_0)+o(u-k_0)}$$
Проинтегрируем уравнение с разделенными переменными:
$${\int }_{x_1}^x\frac{dx}{x}={\int }_{k_1}^k\frac{du}{f(u)-u}$$
Для левого интеграла получаем:
$${\int }_{x_1}^x\frac{dx}{x}=\ln |x|-\ln \left|x_1\right|$$
Для правого интеграла получаем:
$${\int }_{k_1}^k\frac{du}{f(u)-u}=\frac{1}{f^{\prime }\left(k_0\right)-1}(\ln |u-k_0|-\ln |k_1-k_0|)$$
Рассмотрим теперь два случая:
1) $f^{\prime }(k_0)<1$.
Тогда $\ln |x|-\ln \left|x_1\right|\to -\mathrm{\infty }$ при $x\to 0$, а $\ln |u-k_0|-\ln |k_1-k_0|\to -\mathrm{\infty }$, при $u\to k_0$.
Поскольку ${\displaystyle \frac{1}{f^{\prime }\left(k_0\right)-1}}<1$, получаем:
$$\frac{1}{f^{\prime }\left(k_0\right)-1}(\ln |u-k_0|-\ln |k_1-k_0|)\to +\mathrm{\infty }$$
Таким образом:
$$\begin{array}{l}{\int }_{x_1}^x\frac{dx}{x}\to -\mathrm{\infty }\text{ при }x\to 0\\ {\int }_{k_1}^u\frac{du}{f(u)-u}\to +\mathrm{\infty }\text{ при }u\to k_0\end{array}$$
Равенство интегралов невозможно, следовательно никакая интегральная кривая не может касаться прямой $y=k_{0}x$ в начале координат.
2) $f^{\prime }(k_0)>1$.
Тогда:
$${\int }_{k_1}^u\frac{du}{f(u)-u}\to -\mathrm{\infty }\text{ при }u\to k_0$$
Cледовательно любая интегральная кривая касается прямой $y=k_{0}x$ в начале координат.