Задача 70. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям

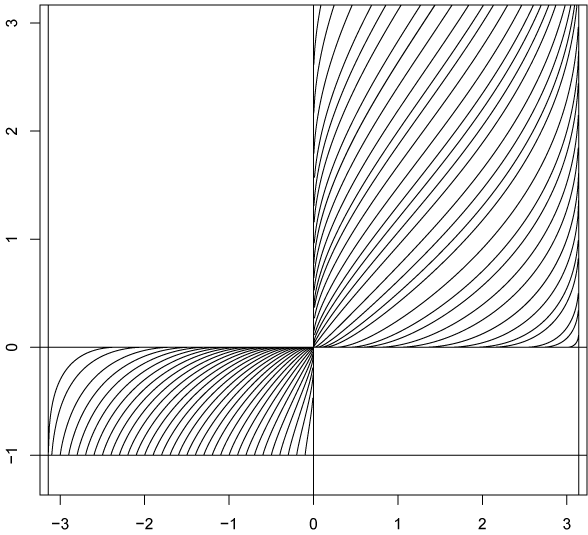
Исследовать поведение интегральных кривых уравнения $y^{\prime }=\sqrt{\frac{\ln (1+y)}{\sin x}}$ в окрестности начала координат. Показать, что из каждой точки границы первого координатного угла выходит одна интегральная кривая, проходящая внутри этого угла.

Решение
1. Найдем область определения функции $\sqrt{\frac{\ln (1+y)}{\sin x}}$
Подкоренное выражение должно быть больше либо равно нулю:
$$\frac{\ln (1+y)}{\sin x}\ge 0$$
Для выражения $\ln (1+y)$ получаем $y>-1$, при этом знак $\ln (1+y)$ зависит от $y$, и $\ln (1+y)>0$ при $y>0$ и $\ln (1+y)<0$ при $-1<y<0$.

Из знаменателя дроби получаем $\sin x\ne 0$, следовательно $x\ne n\pi$.

Получаем, чтобы подкоренное выражение было больше либо равно нулю:
для $y⩾0$, $\sin x>0$ $\Rightarrow$$2n\pi <x<(2n+1)\pi$
для $-1<y⩽0$, $\sin x<0$ $\Rightarrow$$(2n+1)\pi <x<2(n+1)\pi$
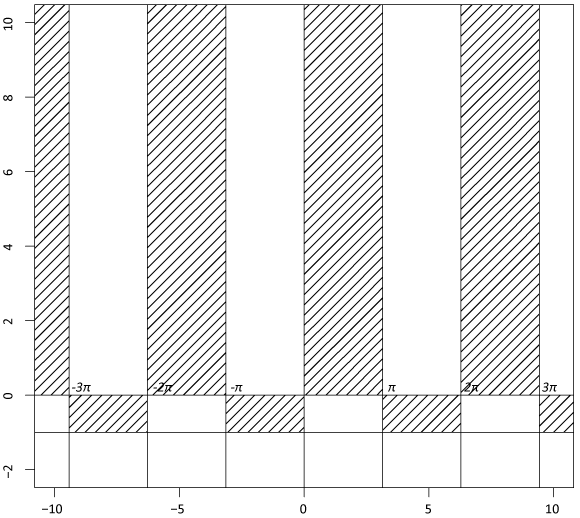
Таким образом, область определения:
$$D=\{2n\pi <x<(2n+1)\pi ,0⩽y<+\mathrm{\infty }\}\cup \{(2n+1)\pi <x<2(n+1)\pi ,-1<y⩽0\}$$

Изобразим область определения:

2. Рассмотрим поведение интегральных кривых уравнения в окрестности начала координат.
Для $0<x,x_0<\pi ,0⩽y<+\mathrm{\infty }$:
Разделяя переменные и интегрируя получим:
$${\int }_{x_0}^x\frac{dx}{\sqrt{\sin x}}={\int }_0^y\frac{dy}{\sqrt{\ln (1+y)}}$$
Интеграл ${\displaystyle {\int }_0^y\frac{dy}{\sqrt{\ln (1+y)}}}$ сходится, и ${\displaystyle {\int }_0^y\frac{dy}{\sqrt{\ln (1+y)}}>0}$.
Соответственно:
$${\displaystyle {\int }_{x_0}^x\frac{dx}{\sqrt{\sin x}}>0}$$
Это означает, что $x>x_0$. Учитывая что производная $y^{\prime }=\sqrt{\frac{\ln (1+y)}{\sin x}}$ всегда больше нуля, получаем что $y=y(x)$ возрастает с возрастанием $x$. Следовательно интегральная кривая стремится вверх вправо. Учитывая что интеграл ${\displaystyle {\int }_{x_0}^x\frac{dx}{\sqrt{\sin x}}}$ сходится при $x\to \pi$, то $y$ стремится к конечному пределу при $x\to \pi$.
Из исходного уравнения $y^{\prime }=\sqrt{\frac{\ln (1+y)}{\sin x}}$ получаем, что при $x\to 0$ производная $y^{\prime }\to +\mathrm{\infty }$, при $x\to \pi$ производная $y^{\prime }\to +\mathrm{\infty }$.

Получаем: интегральные кривые стремятся вверх вправо, асимптотически приближаясь к прямой $x=\pi$.

Для $-\pi <x,x_0<0,-1<y⩽0$:
Разделяя переменные и интегрируя получим:
$${\int }_{x_0}^x\frac{dx}{\sqrt{-\sin x}}={\int }_0^y\frac{dy}{-\sqrt{\ln (1+y)}}$$
Так как $y<0$, интеграл справа отрицательный, следовательно, $x<x_0$. Получается, интегральная кривая стремится вниз влево.
Из исходного уравнения $y^{\prime }=\sqrt{\frac{\ln (1+y)}{\sin x}}$ получаем, что при $x\to -\pi$ производная $y^{\prime }\to +\mathrm{\infty }$, при $y\to -1$ производная $y^{\prime }\to +\mathrm{\infty }$.

Получаем: интегральные кривые стремятся вниз влево, асимптотически приближаясь к прямым $x=-\pi$ или $y=-1$, причем к прямой $x=-\pi$ приближаются по касательной, а к прямой $y=-1$ перпендикулярно.

Построим интегральные кривые:

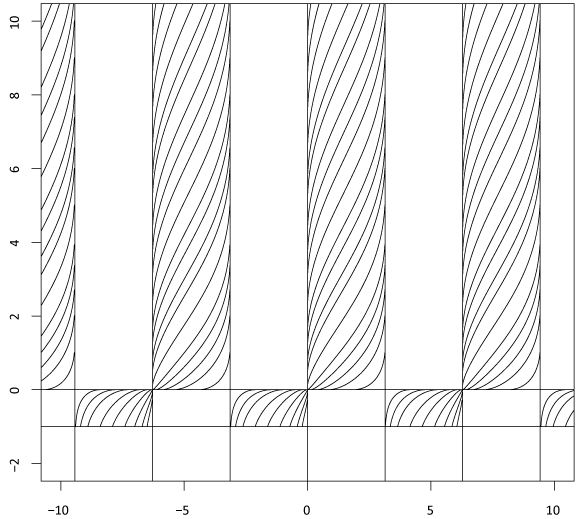
В окрестности начала координат: